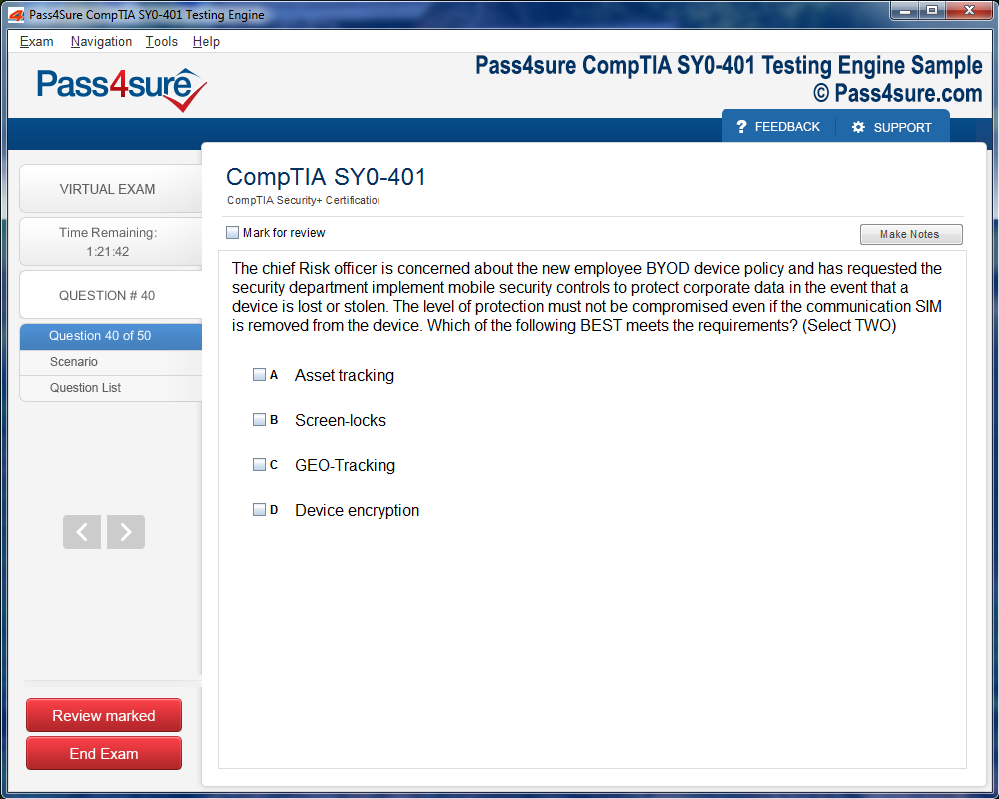
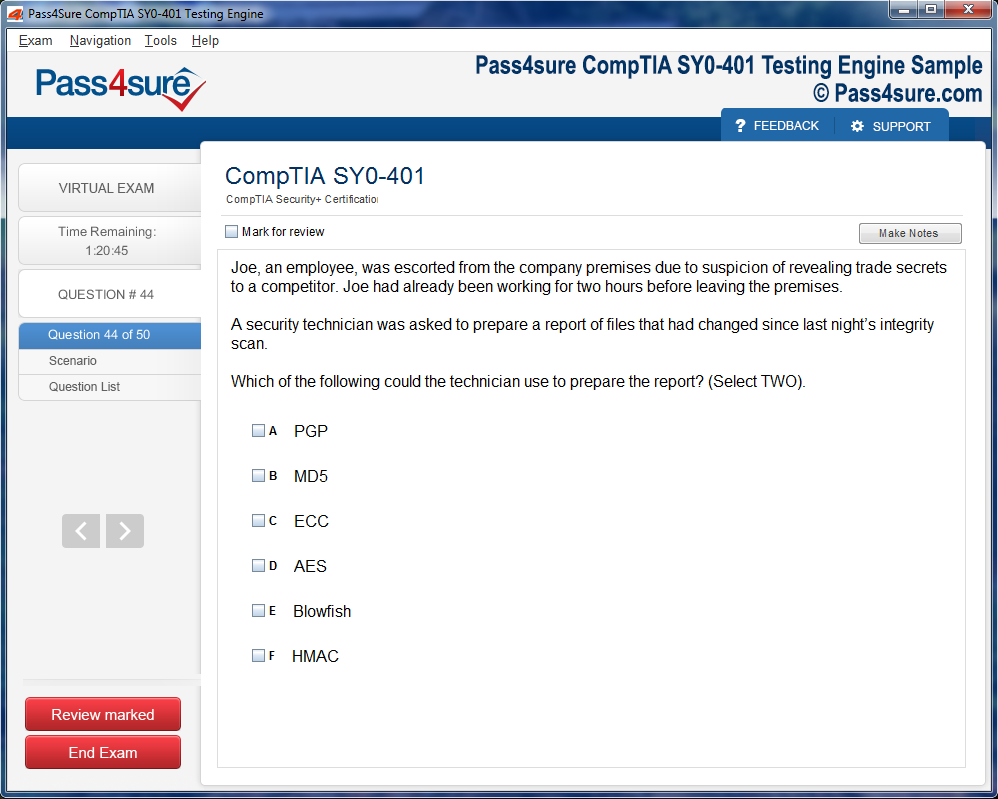
Test Name: THEA - Texas Higher Education Assessment
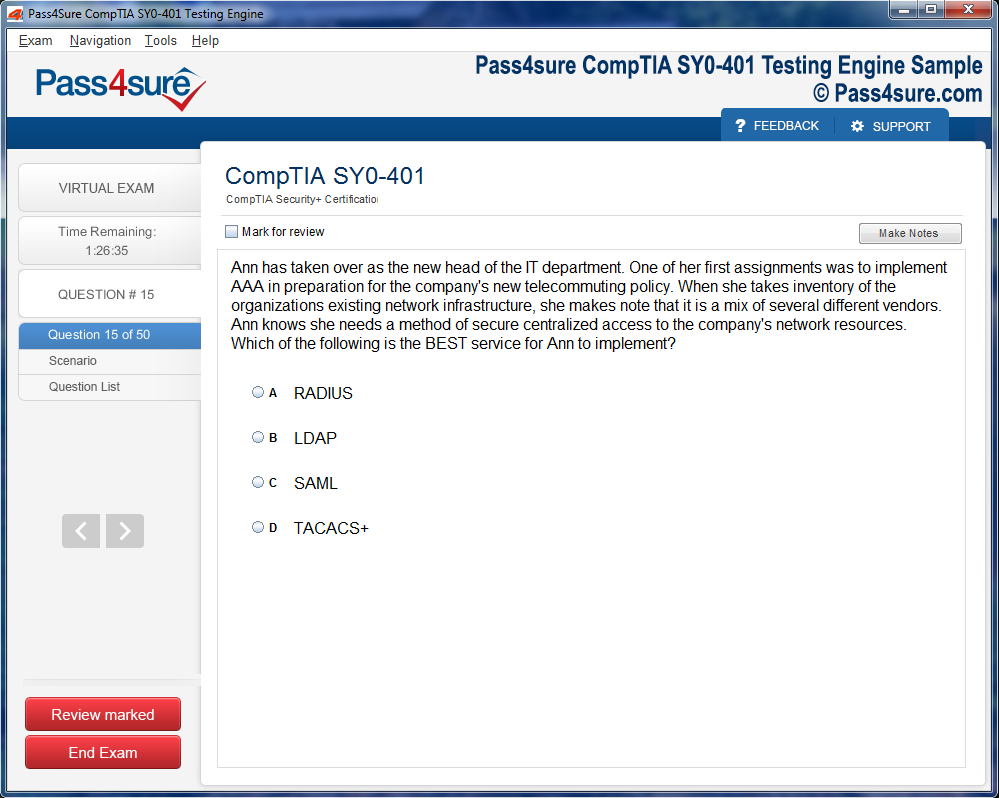
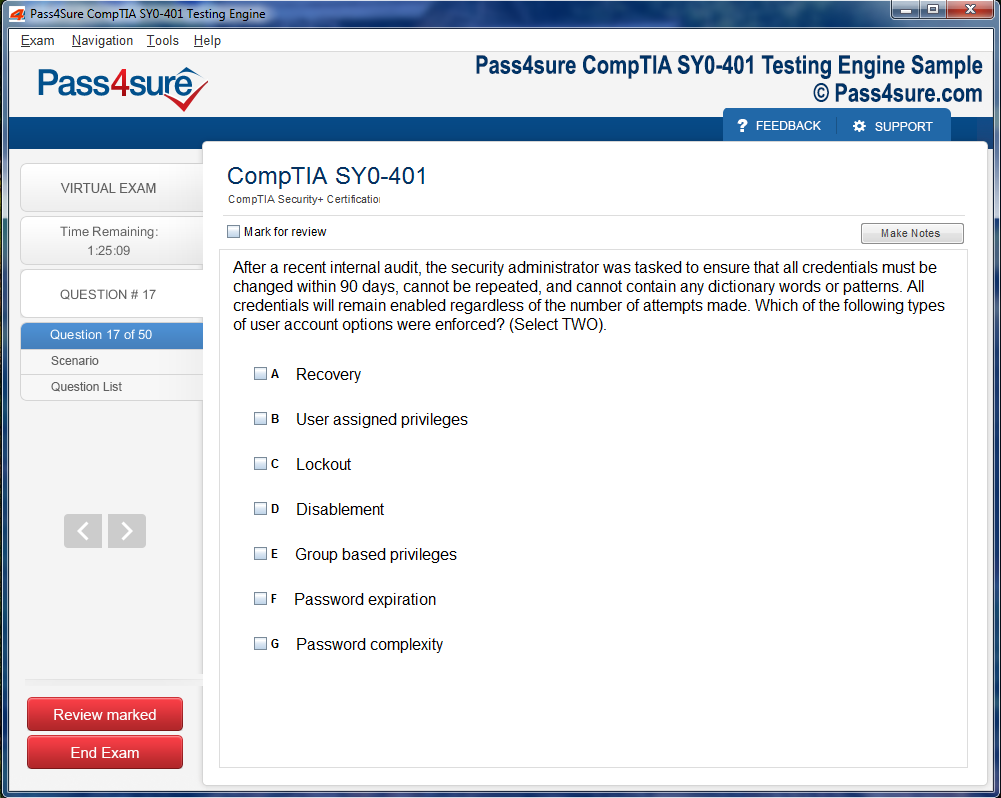
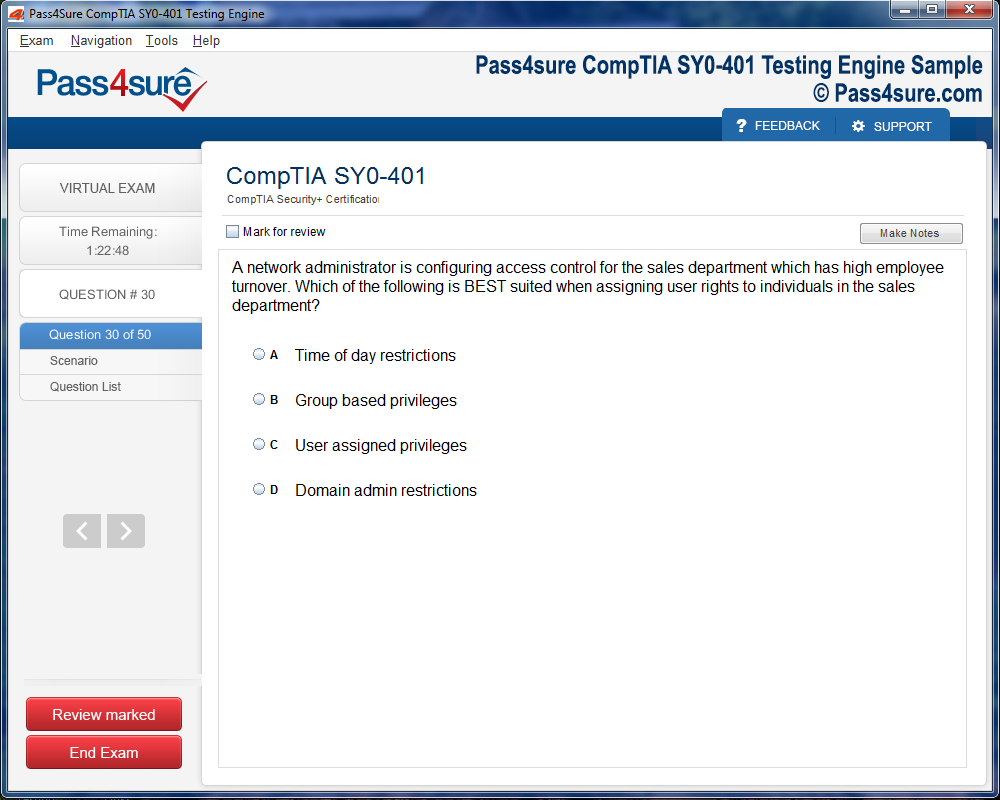
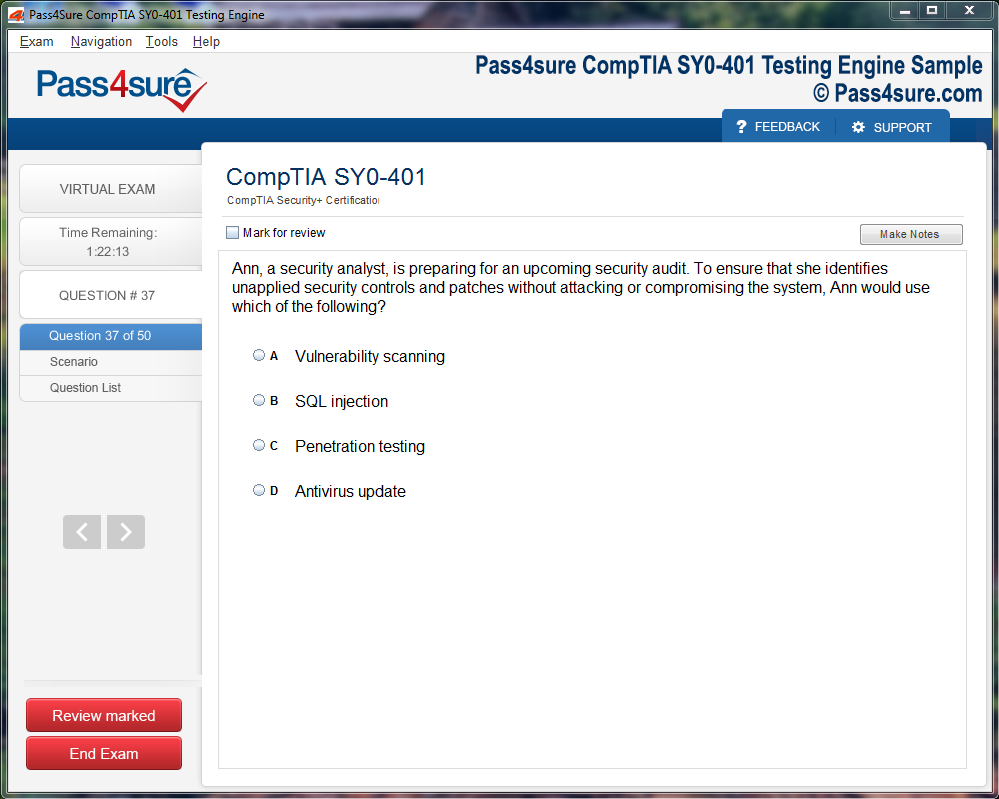
Product Screenshots
The Ultimate THEA Prep Guide for Texas Students
Reading comprehension on the THEA is more than scanning words on a page; it is the art of deciphering layers of meaning, tone, and subtle nuance. Each passage offers a miniature universe, waiting to be explored with patience and curiosity. Students who approach text with an analytical mindset discover connections that may initially seem invisible. By examining word choice, sentence structure, and paragraph flow, learners begin to perceive the underlying argument or narrative the author constructs.
Comprehension is strengthened when readers actively interact with the text. Highlighting key ideas, mentally summarizing paragraphs, and predicting the next logical point can transform reading into a dynamic process. The THEA rewards those who can detect inference and implication rather than merely recalling explicit facts. By practicing with diverse material—from historical documents to contemporary essays—students enhance flexibility and adaptability, two traits that prove invaluable on test day.
Fluency in comprehension also relies on expanding the mental library of vocabulary and expression. Understanding context, identifying tone shifts, and discerning the author’s purpose equip students with tools to answer even the trickiest questions confidently. The challenge lies not in the number of words one knows but in the ability to connect ideas and read between the lines. With steady practice, what once seemed opaque becomes increasingly transparent, and reading transforms from a chore into an engaging intellectual exploration.
Elevating Writing Skills: From Thoughts to Coherent Expression
Writing on the THEA requires the delicate balance between clarity and creativity. Essays are not meant to impress with ornate language but to convey ideas logically and persuasively. A well-crafted essay demonstrates organization, cohesion, and a natural flow that leads the reader through a thought process seamlessly. Students who cultivate habits of planning before writing—outlining main points and supporting details—often find their ideas manifest with precision and ease.
The beauty of effective writing lies in simplicity. Complex ideas need not be tangled in complicated phrasing; they gain strength when presented straightforwardly. Each paragraph serves a purpose, linking back to a central thesis while progressing the argument thoughtfully. Repetition of practice essays builds not just skill but confidence, enabling students to articulate opinions with fluency and authority. Mechanics, grammar, and punctuation are the skeleton that supports content, ensuring ideas stand firm and coherent without distraction.
Critical to writing success is the ability to revise and reflect. The first draft may contain errors or awkward transitions, but subsequent reviews refine clarity and sharpen reasoning. Through reflection, students learn to anticipate questions a reader might ask, strengthening both persuasiveness and accuracy. Writing becomes less a task of mere completion and more a craft of deliberate expression, where ideas are carefully sculpted and polished until they shine with clarity.
Numerical Reasoning: Beyond Numbers
Mathematics on the THEA often intimidates, but its essence lies in logical reasoning rather than rote calculation. Each problem presents an opportunity to decode patterns, identify relationships, and apply principles methodically. Students who internalize problem-solving steps find that even complex questions can be unraveled with patience and structure. Algebra, geometry, and numerical reasoning are not isolated disciplines but interconnected components of a greater analytical language.
Confidence in math develops through deliberate practice and reflection on solutions. Mistakes are not setbacks but invitations to understand the underlying reasoning more deeply. By retracing steps, identifying where logic faltered, and testing alternative strategies, learners cultivate resilience and insight. Repetition strengthens neural pathways, turning once-daunting formulas into familiar tools ready to wield under timed conditions.
Time management in mathematics is particularly crucial. Spending too long on a single problem risks diminishing returns, while too quick a pace may result in careless errors. Balanced pacing, combined with strategic judgment, ensures students maximize accuracy and efficiency. Over time, problem types become recognizable, strategies instinctive, and the anxiety surrounding numerical reasoning gradually dissipates. Mathematics, in this sense, transforms from an obstacle into a language of logic that students can read fluently.
Building Mental Endurance: Preparing for the Long Haul
The THEA is as much a test of mental stamina as of academic skill. Long exams challenge focus, patience, and the ability to maintain clarity under pressure. Students who practice sustained attention during preparation sessions discover that endurance is cultivated gradually, like a muscle strengthened through repetition. Simulated exam conditions, where reading, writing, and math sections are practiced consecutively, mirror the physical and cognitive demands of the actual test.
Mindset plays a pivotal role in sustaining endurance. Those who approach preparation with curiosity and a sense of growth maintain energy longer and recover from setbacks more quickly. Energy management includes not only mental focus but also physical readiness. Adequate sleep, hydration, and nutrition enhance concentration and reduce fatigue. Through repetition and structured study schedules, students gradually build the capacity to maintain high-level cognitive performance across hours of examination.
Developing a rhythm in preparation also contributes to endurance. Alternating between tasks, taking short mental breaks, and returning with renewed attention prevents burnout and keeps the mind alert. Over time, these habits form an internal discipline that serves not only the THEA but also the broader challenges of higher education, where persistence and resilience are as critical as knowledge itself.
Strategic Time Management: Rhythm and Efficiency
Time is a silent adversary in every exam. The THEA rewards those who manage it wisely, balancing speed with careful consideration. Each section requires students to make decisions about how long to spend on questions, when to move on, and when to pause for reflection. Mastering this rhythm is crucial for maximizing performance without sacrificing accuracy.
Practicing under timed conditions trains students to develop an internal sense of pacing. Short drills, progressively longer exercises, and full-length simulated exams create familiarity with the pressure of the clock. Over time, pacing becomes second nature, reducing stress and freeing cognitive resources for problem-solving and comprehension. Strategic time management is not merely about speed; it is about optimizing energy and focus, ensuring that each minute contributes meaningfully to progress.
Beyond the mechanics of timing, strategic thinking is equally important. Not all questions carry the same weight or difficulty. Students learn to identify where effort yields the greatest returns, approaching problems in a way that maximizes both accuracy and efficiency. This combination of tactical judgment and consistent pacing transforms what could be a harrowing experience into a controlled, confident performance.
Cultivating a Growth Mindset: The Secret to Sustainable Success
Perhaps the most profound aspect of THEA preparation is mindset. Students who embrace growth rather than perfection flourish in their studies and in the exam itself. They view errors as opportunities to refine understanding and treat challenges as invitations to learn more deeply. This perspective transforms frustration into motivation and effort into mastery.
The growth mindset nurtures persistence, encouraging students to continue despite setbacks. By focusing on progress rather than immediate results, learners build resilience and confidence. Each practice session, mistake, and insight accumulates into a tangible trajectory of improvement. Success becomes a natural outcome of consistent effort, reflection, and adaptability rather than a product of luck or innate ability.
Support and environment reinforce this mindset. Collaborative study, encouragement from mentors, and exposure to diverse problem-solving approaches enhance both confidence and understanding. Students who internalize the belief that learning is a journey, not a test of fixed ability, unlock the full potential of preparation. With persistence, deliberate practice, and a positive attitude, the seemingly formidable THEA transforms into an arena for growth, skill demonstration, and personal achievement.
Excelling in THEA Mathematics: Turning Numbers into Confidence
Mathematics on the THEA exam is not a measure of genius but a reflection of readiness. It reveals how well students can interpret patterns, reason through numerical challenges, and apply concepts with clarity. Many Texas learners enter this section with hesitation, imagining endless formulas and calculations, but the truth is far simpler. The math portion rewards understanding over memorization. Those who learn to see numbers as ideas rather than obstacles soon discover that confidence is the true formula for success.
The exam covers topics most students have encountered before, yet the way these topics appear can feel unfamiliar. Instead of straightforward problems, the questions often ask for reasoning, connection, and application. Students who grasp why a rule works rather than just how to use it adapt faster to new problem types. Building mathematical confidence begins by rebuilding the relationship between numbers and meaning. Each symbol on the page represents logic, and logic is something every student can master.
The first key to success lies in comprehension. Mathematics is a language, one with its own grammar, structure, and rhythm. Just as in reading comprehension, the challenge is not to memorize but to interpret. A word problem is a short story with numerical characters. Understanding what the question truly asks determines everything that follows. By slowing down to restate the problem in simple words, students allow their reasoning to align with the mathematics behind it. This simple act prevents careless mistakes and brings clarity where confusion once lived.
Building Foundations of Mathematical Understanding
Every powerful structure rests upon a stable foundation, and so does mathematical thinking. The arithmetic skills learned early in school—addition, subtraction, multiplication, and division—remain the pillars supporting algebra and geometry. Students who revisit these basics strengthen their mental framework. Practicing quick calculations, estimating values, and checking reasonableness of answers nurtures precision. When computation feels automatic, the mind is free to focus on analysis rather than arithmetic struggle.
Fractions, decimals, and percentages form another essential triad. They appear constantly throughout the THEA exam, often in disguise. A fraction may become a ratio, a percentage may represent change, or a decimal may measure distance or data. Students who can move comfortably among these forms possess flexibility, a quality that saves time during testing. This skill grows through practice—converting decimals to fractions, estimating percentages, and comparing values until patterns become intuitive. Once mastered, these conversions turn into second nature, freeing energy for deeper reasoning.
Equally vital is understanding proportions and ratios. These concepts appear everywhere from scale drawings to real-world word problems. They teach students to think relationally, not absolutely. Instead of seeing two numbers as isolated, ratios invite recognition of their connection. Seeing 2:5 not as mere digits but as a relationship expands thinking from calculation to comprehension. The more students view numbers as relationships, the more gracefully they can adapt to complex problem types on the THEA exam.
Developing Algebraic Fluency and Logic
Algebra often feels intimidating because it replaces familiar numbers with letters, but those letters are only placeholders for possibilities. Algebra teaches the art of abstraction—how to reason about relationships rather than fixed quantities. On the THEA exam, algebraic reasoning is central. It assesses whether students can form and manipulate equations to express a situation’s essence.
Fluency in algebra begins with understanding equality. Every equation balances two sides like a scale. Each operation must preserve that balance. When students internalize this symmetry, solving becomes less about steps and more about harmony. Moving a term across the equal sign is not a mechanical act but a logical consequence. It reflects the equilibrium that underlies all mathematical structure.
Linear equations, inequalities, and systems of equations test how well students can model and interpret relationships. They reveal not only numerical skill but clarity of thought. Graphs transform abstract ideas into visual forms. A line is not merely a drawing but the trace of a consistent relationship. Recognizing slope and intercept as measures of change and origin brings these lines to life. Instead of memorizing formulas, successful students learn to visualize relationships. This visualization converts algebra into intuition.
Beyond linear relationships, quadratic expressions introduce curvature and complexity. Understanding how they differ from straight lines shows growth in reasoning. Factoring, completing the square, or applying the quadratic formula are not just methods; they are pathways toward clarity. Each approach tells a different story about structure and solution. As students explore these methods, they develop the ability to select the one most efficient for a given problem. Flexibility becomes a sign of mastery.
The greatest secret of algebra is that it teaches discipline of mind. Each symbol must follow logic; each step must justify itself. Practicing algebra therefore strengthens reasoning beyond numbers. It trains students to think sequentially, to plan before acting, and to verify outcomes. On the THEA exam, this disciplined approach ensures accuracy even under pressure.
Geometry as the Art of Visual Thinking
Geometry transforms mathematics into a visual experience. Where algebra speaks in symbols, geometry speaks in shapes. It asks students to interpret space, measure form, and reason about the unseen through logic and imagination. Many students overlook the power of geometry because it feels distant from everyday life, but in truth, geometry is everywhere. From the symmetry of buildings to the layout of maps, its principles shape perception.
The THEA exam includes questions that test geometric comprehension, measurement, and spatial reasoning. Understanding angles, lines, and shapes is only the beginning. The deeper skill lies in visualization—picturing how pieces fit together. When students learn to imagine transformations, reflections, and rotations, they enter the realm of creative reasoning. Geometry rewards curiosity as much as memorization.
Key relationships such as the Pythagorean theorem or properties of triangles serve as tools for reasoning. They are not facts to memorize but ideas that reveal connection. Recognizing that all right triangles share an underlying harmony of squares and sides turns the theorem into more than a rule—it becomes a pattern of truth. Circles, polygons, and three-dimensional figures extend this pattern into greater complexity. Understanding area, perimeter, and volume trains the eye to measure space intuitively.
Coordinate geometry merges algebra with shape, proving that mathematics is not divided but unified. A point on a plane becomes a pair of numbers, and a line becomes an equation. Students who understand this bridge between the visual and symbolic move fluidly across different question types. They realize that math is not about categories but about coherence.
Problem Solving and Mathematical Reasoning
Problem solving is the soul of mathematics. It transforms knowledge into power. The THEA exam challenges students to apply concepts to new situations, testing not memory but adaptability. This section distinguishes those who have learned formulas from those who have learned thinking. A student who understands principles can face unfamiliar problems with calm confidence.
Effective problem solvers share a common trait: they approach every question with patience. Rushing leads to oversight. Instead, they read carefully, restate in their own words, and identify what information is given and what is required. This mental organization transforms complexity into clarity. Once the structure of the problem is clear, the path to the answer reveals itself naturally.
Mathematical reasoning grows through curiosity. Asking why a solution works deepens understanding far more than repeating it. When students check their results and trace their steps backward, they reinforce logic. Each problem becomes a conversation between mind and method. The more they engage with that conversation, the sharper their reasoning becomes.
Word problems test the ability to translate language into mathematics. They require comprehension, not just calculation. Students who can identify relationships within sentences—quantities, changes, comparisons—build equations that mirror real-life reasoning. Practice with these problems strengthens both reading and logic, uniting the verbal and numerical sides of intelligence.
Data interpretation, charts, and tables often appear in the THEA mathematics section. They test analytical agility rather than computation. Recognizing patterns, trends, and relationships within data builds confidence in navigating complex information. Students can practice by analyzing everyday statistics—weather data, sports scores, or surveys—to develop comfort with extracting meaning from numbers. Over time, numbers cease to intimidate and begin to speak.
Time Management and Testing Strategy
Mathematical understanding means little without the ability to apply it within time limits. The THEA exam demands focus, composure, and pacing. Students must learn to distribute time wisely, neither rushing through nor dwelling too long on a single question. Practicing timed problem sets develops intuition for pacing. The goal is balance—enough time for reflection, yet steady progress through the section.
One useful technique is to begin with questions that appear manageable. Success builds momentum, and momentum sustains confidence. As students progress, they should mark challenging items for later review rather than losing time in frustration. This approach keeps the rhythm of testing steady and the mind calm. Often, when returning to a difficult question later, clarity emerges naturally because the subconscious continues processing in the background.
Estimation is another powerful time-saving skill. Before calculating precisely, approximating the answer provides direction. It prevents errors caused by misinterpretation and helps eliminate obviously incorrect choices quickly. Estimation sharpens intuition about number size and reasonableness. A student who can sense whether an answer feels right is less likely to fall into traps of miscalculation.
Checking work is equally important. Even strong reasoning can falter through small slips in arithmetic. When time allows, students should review answers, especially those involving multiple steps. Reversing operations or substituting results back into equations confirms correctness. Accuracy comes not only from intelligence but from carefulness.
Mental composure is the hidden foundation of success. Mathematics often triggers anxiety, but calm thinking multiplies accuracy. Deep breathing before beginning, maintaining posture, and approaching each problem with curiosity rather than fear changes everything. Confidence grows not from perfection but from preparation and presence of mind. When students see each problem as an opportunity to think rather than a threat, performance naturally improves.
Cultivating Daily Practice and Mathematical Mindset
Excellence in mathematics is built through steady habit rather than sudden mastery. Daily engagement, even for short sessions, strengthens familiarity and endurance. Just as athletes train muscles, students train thought patterns. Solving a few problems each day, reflecting on mistakes, and exploring different methods create lasting improvement.
The most transformative practice comes from understanding errors. Every mistake hides a lesson. When students review their missteps thoughtfully—asking what assumption failed or what pattern they overlooked—they replace frustration with insight. This mindset turns struggle into progress. Over time, repeated reflection builds a deep, flexible understanding that cannot be shaken by surprise questions.
Mathematical confidence is born from consistency. Small victories accumulate until the subject no longer feels foreign. Reading math-related articles, exploring puzzles, or applying numbers to personal interests reinforces engagement. The goal is to make mathematics part of daily thought, not just a school requirement. When curiosity replaces obligation, learning accelerates naturally.
A growth mindset transforms preparation into progress. Believing that ability expands through effort changes how students respond to difficulty. Instead of thinking they are “not math people,” they realize that every new concept is learnable through persistence. This belief, supported by practice, creates resilience. On exam day, resilience becomes as important as skill.
Connecting Mathematical Skills to Real-Life Thinking
The purpose of mathematics extends beyond the classroom or test. It is a way of perceiving and solving problems in the world. The reasoning developed through equations, patterns, and measurements enhances decision-making in daily life. Budgeting, planning, analyzing information—all draw from the same logical structure that the THEA exam measures.
When students connect what they study to real-world experiences, retention strengthens. Percentages become meaningful when seen in financial discounts or data reports. Geometry becomes practical when applied to design or navigation. Algebra becomes useful when planning schedules or comparing rates. Every connection made between numbers and life deepens comprehension.
Understanding this relevance changes motivation. Students prepare not only to pass an exam but to sharpen their reasoning for life beyond it. Mathematics becomes a tool of empowerment, a lens for understanding structure and pattern everywhere. Seeing it as a living language rather than a static subject infuses learning with energy.
This shift in perspective also brings emotional confidence. Numbers lose their power to intimidate. They become allies in problem-solving, not enemies to overcome. When students realize that the logic behind mathematics mirrors the logic of life—analyzing, planning, adapting—they carry that clarity into every decision they make.
Elevating Mathematical Expression and Analytical Clarity
Beyond computation lies the artistry of explanation. The THEA exam often includes reasoning questions that require interpreting rather than calculating. Here, clarity of thought becomes visible through words. Students who can describe how they arrived at an answer demonstrate mastery that mere numbers cannot show. This ability to express logic clearly distinguishes strong thinkers.
Practicing explanation, even silently, sharpens reasoning. When students solve a problem, they can imagine teaching it to someone else, describing each step aloud or on paper. Doing so reveals gaps in understanding and solidifies learning. Mathematics communicated becomes mathematics understood. This reflective habit deepens both precision and memory.
Analytical clarity also grows through pattern recognition. Recognizing symmetry, repetition, and structure in problems allows quicker insight. The mind learns to predict outcomes and anticipate methods. Over time, solving becomes smoother, almost musical. Each problem unfolds like a melody, guided by logic and rhythm. This sense of flow transforms testing from stress into challenge—a mental game rather than a battle.
Clarity is not about speed alone but about coherence. Even when time is short, a clear thinker proceeds step by step, trusting logic over haste. This calm focus becomes visible in performance. Students who cultivate such clarity find that mathematics no longer feels like a maze but a map—one they can read with confidence.
The Foundation of Mathematical Understanding
Mathematics is often perceived as a realm of mystery, yet it is the purest form of logic humans have ever crafted. Every symbol, every equation, every pattern of numbers follows a structure that has existed since the dawn of reason. The key to excelling in THEA mathematics lies not in memorizing mechanical steps but in cultivating a relationship with numbers so natural that reasoning becomes instinctive. When students learn to see the flow of relationships within mathematical expressions, their confidence grows organically, transforming fear into understanding. The THEA mathematics section measures fundamental reasoning, not extraordinary genius. It examines how a mind perceives relationships between values, shapes, and proportions. By nurturing a calm and observant mindset, anyone can master its rhythm.
Mathematics is a conversation between the learner and the universe. The moment one realizes that every problem has a logical conclusion, anxiety begins to dissolve. At first, numbers may appear cold and distant, yet with consistent engagement, they begin to reflect clarity. A learner who respects the process of discovery soon finds beauty in balance, precision, and structure. This shift—from intimidation to appreciation—creates a foundation upon which true confidence is built. To excel in THEA mathematics, one must start small but think deeply, exploring each rule as a piece of an intricate, perfectly balanced puzzle. Every correct answer becomes a note in a growing symphony of logic.
Reclaiming Comfort with Arithmetic
The heart of mathematics rests upon basic arithmetic. Without fluency in addition, subtraction, multiplication, and division, higher concepts lose their strength. It is astonishing how often advanced confusion comes from small slips in fundamental computation. Mastery of the basics transforms complexity into simplicity. Arithmetic is not just the act of combining or separating numbers; it is the language that describes quantity. When students rebuild their relationship with these core operations, they prepare the ground for algebraic and geometric reasoning to flourish. Arithmetic demands precision but rewards intuition. Repetition strengthens memory, and memory nurtures speed.
Fractions and decimals often intimidate learners, yet they are only two expressions of the same concept—parts of a whole. Those who understand how to glide smoothly between them gain efficiency in every section of the THEA mathematics test. Fractions are about relationships; decimals are about position. The moment a student realizes this, accuracy improves naturally. One need not memorize endless conversion tricks; understanding the pattern beneath them suffices. Arithmetic also thrives on patience. Each correct computation carries a quiet satisfaction, a sign that the mind and the numbers have achieved harmony.
Arithmetic practice should never feel mechanical. It should feel alive, almost musical. The regular beat of multiplication tables, the symmetry of long division, and the rhythm of number patterns together create a sense of control. When these fundamentals become second nature, learners can focus on reasoning instead of remembering. It is at this stage that mathematics begins to breathe, that numbers cease to be obstacles and instead become companions guiding toward clarity.
Building Balance through Algebra
Algebra is the turning point where numbers gain motion. Here, quantities interact, change, and relate to one another in more abstract ways. Many learners initially see algebra as a labyrinth of letters and symbols, yet its foundation is balance. Every equation is a story of equilibrium—what exists on one side must remain equal to what exists on the other. Once a learner internalizes this truth, algebra transforms from confusion into conversation. Solving for a variable becomes the act of restoring harmony. Each manipulation of terms is a small step toward discovering order hidden beneath symbols.
To master algebra for the THEA test, students must treat each equation as a system that seeks calmness. The process of isolating variables, simplifying expressions, and solving linear or quadratic equations becomes a rhythm that the mind can follow with comfort. When algebra feels overwhelming, returning to the principle of equality renews focus. If you add something to one side, add it to the other; if you divide, divide equally. This sense of fairness underlies every algebraic move. It is not memorization but respect for balance that creates success.
Expressions, exponents, and inequalities further extend this balance. They test not just mechanical skill but interpretive reasoning. Simplifying expressions asks the learner to see structure within chaos. Working with exponents reveals the elegance of repetition within growth. Inequalities remind the student that not all relationships are identical, but all are governed by reason. The learner who grasps these subtle truths finds that algebra becomes an ally—a steady tool for problem-solving that nurtures composure even under timed conditions. Algebra, once feared, becomes a mirror reflecting the precision of thought itself.
Visual Reasoning through Geometry
Geometry brings mathematics into vision. While algebra speaks in symbols, geometry speaks in shapes. It allows the learner to visualize balance, symmetry, and proportion. Understanding geometry for the THEA exam is not about memorizing a library of formulas; it is about grasping how shapes relate to one another through space and measure. A triangle’s strength, a circle’s perfection, or a line’s simplicity all reveal mathematical truths that the human eye can sense long before computation begins. The learner who trains to sketch, to see patterns, and to imagine the unseen edges of a figure, develops a reasoning power that transcends formulaic thinking.
The Pythagorean theorem, one of geometry’s timeless treasures, captures this principle. It describes not only the relationship between sides of a right triangle but also the constancy of proportion across all shapes and distances. Likewise, the properties of angles, areas, and perimeters are reflections of this same harmony. To excel, students should learn to draw as they think. A simple sketch converts abstract words into visible relationships. Lines become guides, circles become measures, and angles become insights. With practice, geometry ceases to be intimidating—it becomes a form of visual poetry.
Geometry also strengthens logical thought in daily life. Measuring space, estimating distance, understanding layout—all of these practical skills spring from geometric intuition. On the THEA exam, geometry problems may appear in disguise: sometimes as simple measurements, sometimes as complex figures. In each case, the student who calmly visualizes the situation stands at an advantage. Geometry, when understood, invites curiosity. It invites the learner to look deeper at the world and recognize the quiet geometry of existence—the way buildings stand, shadows fall, and paths intersect. Such awareness feeds mathematical confidence in profound ways.
The Art of Translating Word Problems
Word problems are where mathematics meets language, and for many learners, this meeting creates friction. The key to mastering them is to slow the reading process and translate ideas into equations step by step. Word problems often conceal simple operations beneath layers of context. The challenge is not computation but comprehension. The most successful students do not rush; they rephrase the scenario in plain language until the meaning becomes transparent. Once the situation is understood, forming an equation is easy. The words are merely the story; the math is the structure beneath the story.
To excel in this area, learners must practice active interpretation. Every sentence in a problem carries information—some essential, some decorative. Separating the necessary from the distracting is a skill that grows with deliberate practice. Reading carefully, underlining key numbers, and restating the question in one’s own words are effective habits. When a learner turns text into a clear numerical relationship, half the work is already done. The rest is pure reasoning.
This process reflects more than mathematical understanding; it cultivates patience and linguistic clarity. The connection between language and logic becomes visible. A student who once felt overwhelmed begins to realize that words can no longer confuse if they are read with intent. Word problems are opportunities to strengthen both verbal and analytical skills simultaneously. With time, the mind learns to hear mathematics even in ordinary speech—to recognize that every description hides a measurable truth. That is where mastery truly begins.
Interpreting Data with Clarity
Modern mathematics is not limited to numbers or shapes alone; it also embraces information. Data interpretation has become a central component of assessments like the THEA because it measures how efficiently one can read, analyze, and reason about quantitative information. Graphs, tables, and charts are forms of storytelling where numbers replace words. To understand them is to listen to patterns. The first step in mastering data interpretation is observation. Before calculating, the learner must simply see—what trends appear, what comparisons are implied, what scales are presented.
The ability to extract meaning from visual data strengthens with habit. Learners should train themselves to examine every axis, every label, and every relationship. Often, the answer hides not in computation but in recognizing patterns—a rise, a decline, a steady line. The key is to avoid assumptions. Reading data demands neutrality and care. A quick glance may mislead, but a deliberate scan reveals order. Once the message of the graph becomes clear, answering the question feels effortless.
Data interpretation also connects mathematics to daily reality. We see graphs in weather forecasts, budgets, sports statistics, and reports. Each requires the same kind of disciplined attention demanded by the THEA. By practicing this skill, students strengthen not just their test performance but their ability to navigate information in real life. Numbers become not threats but guides, helping one see truth within complexity. The art of interpreting data is the art of perceiving structure in chaos—a skill that transforms uncertainty into insight.
Developing Speed and Strategy through Practice
Confidence in mathematics is born from familiarity, and familiarity grows through consistent, intentional practice. Every learner who aims to master THEA mathematics must embrace repetition not as monotony but as refinement. Timed practice sessions simulate the true conditions of the test and reveal one’s natural rhythm. They teach pacing—the delicate balance between speed and precision. In such sessions, students learn how long to linger on each problem and when to move on. Efficiency becomes instinctive only through repetition. What feels slow at first eventually becomes swift and graceful.
Strategic practice also involves learning to recognize problem types. Most mathematical questions follow patterns. A learner who can quickly identify the structure behind a problem—whether it requires algebraic manipulation, geometric visualization, or data interpretation—saves valuable time. This awareness allows the mind to approach each question calmly, applying the right method immediately. It is not the speed of calculation that determines success but the clarity of recognition.
When errors occur, they are not failures but revelations. Every mistake holds a story about where thought wavered or attention slipped. Reviewing wrong answers with curiosity turns frustration into progress. The student who studies each error and asks what caused it grows rapidly. Over time, accuracy strengthens, and confidence deepens. Mathematical growth is not sudden; it unfolds quietly, through persistence and reflection. Each solved problem, each corrected mistake, adds a layer of certainty.
Cultivating Calmness and Mathematical Composure
The mathematics section of the THEA is not only a test of knowledge but also of emotional steadiness. Even the most skilled learner can falter under tension. Composure is the invisible strength behind every correct answer. Calmness allows reasoning to flow without interference. When stress rises, the mind rushes and clarity fades. Therefore, part of preparation involves learning how to breathe, pause, and think deliberately. This habit transforms panic into focus. During the test, reading each question slowly and verifying understanding prevents careless slips.
Neatness also matters. Writing clearly, aligning steps, and labeling answers reduce confusion. Mathematical order in presentation mirrors mental order in reasoning. The student who practices structured writing practices structured thinking. Confidence emerges not from arrogance but from quiet trust in preparation. It is the knowledge that one has faced challenges, made mistakes, and learned from them. On exam day, that trust steadies the hand and sharpens the mind.
Calmness further extends beyond the test itself. It becomes a way of thinking—a discipline of attention and patience that enriches all forms of reasoning. Mathematics, after all, is not a contest of memory but an exercise in mental clarity. The learner who cultivates calmness discovers that every challenge, whether numerical or personal, becomes more manageable. Each solved problem becomes proof of inner balance. Through such calm persistence, numbers lose their intimidation and instead become silent allies.
Transforming Fear into Mastery
Every student begins the journey toward THEA mathematics with a certain level of unease. Numbers can feel foreign, equations can feel intimidating, and time pressure can make the simplest calculation seem impossible. Yet behind that anxiety lies potential—the potential to transform fear into mastery. The transformation begins the moment one chooses to face mathematics not as an enemy but as a partner. Each problem, each equation, each challenge is an opportunity to think more clearly, to reason more deeply, and to grow more confident. Fear fades when curiosity rises.
This transformation requires patience. Learning mathematics is not about speed; it is about depth. The learner must allow understanding to settle slowly. Practice should be steady, reflective, and honest. Instead of chasing shortcuts, one should nurture comprehension. The joy of understanding why something works is far more lasting than the fleeting relief of memorizing a formula. Through consistent effort, mathematics reveals its generosity—it rewards diligence with clarity. Students who approach it with respect discover that even the hardest problems eventually yield to logic.
Over time, a remarkable shift occurs. The student who once doubted begins to trust. The formulas that once seemed arbitrary now make sense. The diagrams that once confused now appear familiar. The rhythm of computation becomes music, and the mind dances gracefully with numbers. Mathematics becomes not a test of intelligence but a reflection of perseverance. To excel in THEA mathematics is to reach a point where confidence is natural and effort feels harmonious. The numbers, once cold, become warm companions guiding thought toward precision and peace.
Strategic Foundations of Purposeful Preparation
Every great achievement begins with direction. The path toward mastering any examination, including THEA, demands an organized framework rooted in discipline and self-awareness. Success is rarely an accident; it is a deliberate result of structured effort. When learners create a personalized plan, they convert uncertainty into direction and anxiety into confidence. The essence of preparation lies in transforming ambition into measurable actions that progress steadily over time.
A student who studies without order often feels trapped in confusion. Hours slip away without meaningful improvement because energy disperses across unplanned tasks. The disciplined learner, however, sees each day as a calculated move. The mind thrives under structure, responding best when it understands what to expect and when to expect it. Building such a routine nurtures focus, allowing each study period to yield tangible results.
Strategic preparation is not about exhausting oneself but about cultivating endurance. It invites learners to analyze their current standing and build from that truth. By setting clear intentions and aligning habits with goals, even daunting challenges become manageable. Purpose transforms effort into progress, and structure transforms chaos into clarity. The journey begins not with intensity but with intention.
Assessing Strengths and Weaknesses with Honesty
The cornerstone of any successful study plan is self-assessment. Students often rush into memorization, yet true advancement begins with reflection. Knowing where one stands reveals where one must go. Taking a diagnostic assessment is more than a score; it is a mirror showing both brilliance and blind spots. Some sections may already feel effortless, while others seem to resist improvement. Recognizing these differences helps allocate energy wisely.
The temptation to repeat comfortable tasks is strong. It feels satisfying to practice what one already knows. Yet growth hides in discomfort. The sections that challenge most are the ones that demand the greatest attention. Every weakness, when faced with persistence, gradually transforms into a strength. Identifying the exact skill gaps—be it comprehension speed, grammatical precision, or numerical reasoning—creates a targeted approach that eliminates wasted effort.
Reflection should also consider learning style. Some minds thrive on visual aids, others on repetition or storytelling. Understanding how the brain absorbs and retains information makes the study plan not only efficient but also enjoyable. A learner aware of their patterns can adapt study materials to suit them, turning the process into something natural rather than forced. Self-awareness, when combined with strategy, forms the backbone of true preparation.
Designing a Balanced and Sustainable Schedule
Once the foundation of self-knowledge is set, structure follows naturally. A study schedule acts as a compass, guiding the learner through time’s endless distractions. Many students assume success comes from long, intense sessions, yet the mind works best in measured intervals. Concentrated sessions of forty-five minutes, followed by short periods of rest, sustain attention and prevent burnout. It is not the quantity of hours but the quality of focus that determines mastery.
Consistency outweighs intensity. A single, committed hour each day over several months brings far greater results than sporadic bursts of energy. When learning becomes a daily rhythm, it embeds itself in memory. The brain, trained by routine, begins to anticipate focus during study periods, easing the struggle of concentration. Scheduling should remain realistic, matching one’s lifestyle rather than fighting against it.
Equally essential is flexibility. Life’s unpredictability requires a plan that bends but never breaks. Missed sessions should be rescheduled, not abandoned. Even brief reviews during busy days maintain connection with material and prevent regression. A calendar filled with clearly labeled topics—reading comprehension, writing skills, mathematical reasoning—provides visual motivation and order. The schedule becomes both a guide and a promise: that daily discipline will eventually translate into success.
Deepening Focus through Single-Task Learning
In an age of constant distraction, focus is a rare art. Effective learners protect their attention fiercely. Dividing study sessions among multiple subjects weakens retention, while concentrating on a single topic enhances mastery. Each subject requires a distinct mental rhythm, and switching too quickly scatters understanding. Devoting a session exclusively to one area—perhaps essay construction on one day, problem-solving on another—allows the brain to fully engage with that skill.
When the mind immerses completely in a single concept, neural connections strengthen. The learner begins to recognize patterns, relationships, and shortcuts that fragmented attention would never uncover. Mental clarity grows from depth, not breadth. Engaging actively with material—summarizing passages aloud, writing explanations by hand, or mentally teaching concepts to an imagined class—builds long-term understanding.
Every focused session becomes an act of craftsmanship. Learning ceases to be mechanical and turns into creation. Words form meaning, formulas reveal logic, and comprehension deepens naturally. The student learns not merely to recall answers but to think, reason, and articulate. True focus invites mastery because it removes the noise of multitasking and allows only knowledge to speak.
Integrating Practice and Reflection
Practice transforms theory into skill. Yet practice without reflection risks repetition of mistakes. The most efficient learners treat every exercise as a lesson, not merely a task to complete. When working through problems or reading passages, they pause to ask themselves what strategies succeeded and what faltered. Each challenge becomes feedback, and each misstep becomes instruction.
Full-length mock tests mirror real conditions, preparing both mind and body for the rhythm of examination day. Timed assessments build endurance, forcing the learner to think swiftly and efficiently. Once completed, reviewing the test matters more than the score itself. Each incorrect answer reveals a missing piece of understanding. Dedicating time to study those gaps prevents repetition of errors in future attempts.
Reflection after each session consolidates progress. Writing short summaries of what was learned anchors information in memory. Over time, these summaries form a personalized reference guide, filled with individual insights and strategies. Learning becomes an evolving dialogue between experience and awareness. Through consistent practice and reflection, knowledge ceases to be temporary and becomes embedded, ready to surface whenever needed.
Creating an Environment that Nurtures Concentration
External surroundings silently shape internal focus. A cluttered or noisy space fragments thought, while a calm, orderly environment amplifies clarity. The perfect study corner does not require extravagance; it needs intention. A well-lit desk, comfortable seating, and minimal distractions create a sanctuary for learning. The simple act of sitting in the same spot each day signals the brain that it is time for concentration.
Digital distractions often steal attention invisibly. Notifications, messages, and background noise can break mental flow within seconds. Turning off alerts, closing unnecessary tabs, and silencing devices protect mental continuity. Many learners find value in designating a specific study hour, transforming it into a daily ritual. Repetition of this pattern strengthens association—sitting in that chair at that time automatically triggers focus.
The environment extends beyond physical space. It includes mental atmosphere as well. A calm mind enters study with openness, while an anxious one resists. Breathing exercises or short walks before study sessions can reset emotional balance. Over time, this balance creates a state where focus feels effortless, as though the surroundings themselves assist the mind in remaining still and attentive.
Sustaining Motivation through Purpose and Reward
Long-term preparation often tests endurance more than intelligence. Sustaining enthusiasm requires continual reminders of purpose. Every learner must reconnect frequently with the reason behind their effort. Whether it is the dream of advancing education, achieving independence, or proving capability, that inner reason fuels persistence. When the mind understands why it works, discipline becomes devotion.
Small celebrations reinforce this drive. Finishing a challenging topic, improving a test score, or simply maintaining a daily streak deserves recognition. These moments of acknowledgment transform fatigue into satisfaction. Rewarding progress does not require extravagance—sometimes a short rest, a favorite meal, or a peaceful walk serves as perfect encouragement. The act of celebrating keeps motivation alive.
Confidence grows not from perfection but from progression. Every improvement, no matter how minor, strengthens belief in eventual success. Comparing oneself only to one’s past performance eliminates discouragement and fosters steady growth. Motivation is not a constant flame; it flickers. Yet through self-recognition and gentle encouragement, it can be reignited whenever it fades.
Balancing Study with Wellness and Rest
Learning thrives in a healthy body. The mind, though powerful, draws its energy from physical vitality. Exhaustion blurs comprehension, while proper rest sharpens recall and creativity. Sleep, often sacrificed during preparation, is in truth an integral part of it. During rest, the brain organizes memories and strengthens new connections, converting temporary knowledge into lasting wisdom.
Nutrition and hydration equally influence performance. A balanced diet nourishes concentration, while dehydration slows thought. Simple habits such as drinking water regularly and eating wholesome meals ensure mental clarity. Movement also plays a vital role. Gentle exercise refreshes circulation, delivering oxygen to the brain and relieving stress. Even brief stretches between study sessions revive alertness.
Wellness includes emotional balance as well. Overworking leads to mental fatigue, reducing enthusiasm. Taking mindful pauses restores joy in learning. A calm, rested learner absorbs information faster and performs better than one overwhelmed by exhaustion. Health and knowledge intertwine; each sustains the other. When both are nurtured, preparation transforms from strain into harmony.
Adapting Flexibly to Life’s Unpredictability
No plan survives unchanged. Life inevitably introduces interruptions—family duties, unexpected tasks, shifting priorities. The key to lasting success lies in adaptability. A strategic learner does not see obstacles as failures but as adjustments waiting to be made. Flexibility allows continued movement even when routine falters.
A day missed should not dissolve determination. Instead, one can reschedule or modify the workload, redistributing tasks without guilt. The goal is continuity, not perfection. Even on days when time feels scarce, brief reviews maintain mental connection with study material. Consistency of contact matters more than duration of effort.
Adaptability also means adjusting techniques. If a particular study method loses effectiveness, another can replace it. Perhaps audio summaries work better during commutes or digital flashcards during breaks. Evolving strategies keep learning dynamic and engaging. A flexible plan mirrors life itself—resilient, responsive, and always in motion.
Transforming Preparation into a Journey of Mastery
Studying for THEA is not merely about passing an exam; it is about mastering oneself. Through structured planning, honest reflection, focused execution, and balanced living, preparation becomes transformation. The journey disciplines the mind, strengthens patience, and cultivates perseverance. Each deliberate step teaches more than content—it teaches control, awareness, and resilience.
A well-structured study plan turns anxiety into assurance. Students no longer drift through material blindly but move with direction and confidence. The process itself becomes fulfilling, as each hour invested carries visible growth. What begins as an obligation evolves into empowerment. Learning ceases to feel like a burden and starts to feel like a journey toward capability.
This transformation is gradual yet profound. Every schedule revised, every test reviewed, and every challenge faced contributes to inner strength. Time, once feared, becomes an ally. Each moment spent wisely brings the learner closer to readiness. Strategic study does not just prepare one for an examination; it builds the foundation for lifelong learning and self-mastery.
The Calm Before the Challenge
When the day of the exam dawns, the air feels charged with quiet anticipation. Every heartbeat carries echoes of the long journey that led to this moment—hours spent poring over notes, rehearsing practice questions, and imagining success. The mind, after weeks of focus, hovers between excitement and unease. The night before, the wise approach is simplicity. The mind thrives on order, not clutter. Instead of cramming the final fragments of information, relaxation restores clarity. Reading light material, listening to soothing music, or taking a short evening walk helps the brain settle into a tranquil rhythm. Setting out every essential—admission slip, sharpened pencils, erasers, and identification—diminishes the morning chaos that so easily disrupts composure.
Sleep is the silent companion of success. A full night’s rest strengthens concentration and memory far more than last-minute review ever can. The body and mind align best when refreshed, not exhausted. In those quiet moments before sleep, visualization becomes a secret weapon. Picture walking calmly into the testing room, feeling composed, steady, and confident. Such mental rehearsal cultivates assurance that carries into the real experience.
Morning brings light and motion. Breakfast should be balanced, never burdensome. A modest meal with fruit, oats, or protein ensures steady energy. Water refreshes the body, though moderation prevents distraction. The purpose is nourishment, not indulgence. Each choice—every bite, every breath—shapes the mental landscape of the hours ahead.
Entering the Space of Focus
Reaching the testing site early grants the most valuable currency of all: time. Time to breathe, to observe, to adapt. Those who rush arrive burdened with scattered thoughts; those who prepare enter like seasoned travelers. As the testing room fills with quiet shuffling and muted whispers, calm breathing becomes the anchor. The air may feel thick with tension, but slow, deliberate inhalation clears the fog of apprehension.
Before instructions begin, there lies a brief and golden interval—a moment to center the self. Visualize steady hands, clear reasoning, and fluid recall of every concept studied. Confidence is not arrogance; it is quiet readiness. Each test taker who sits tall and trusts their preparation stands already ahead of fear.
When the test opens, the first task is understanding. Reading each direction attentively saves precious minutes and prevents errors born of haste. Each section has its rhythm; forcing speed destroys comprehension. The student who works like a steady metronome—measured and controlled—turns anxiety into mastery.
Rhythm and Resilience in Motion
As questions unfold, moments of doubt inevitably appear. There are always passages that seem perplexing, numbers that refuse to align, choices that blur together. Yet this is not defeat—it is the natural pulse of the test. The secret lies in movement. Mark uncertain questions, breathe, and proceed. Momentum keeps the mind alive. Often, clarity blooms upon return, as if the answer waited quietly beneath the surface.
Mental fatigue creeps slowly, like mist over a valley. The sharp thinker learns to pause briefly without losing pace. Stretching the shoulders, shifting posture, or glancing softly away from the page grants the eyes and brain a brief reprieve. These tiny intermissions renew concentration more effectively than relentless effort. Endurance, not aggression, wins the day.
Time is both ally and adversary. To command it requires awareness, not fear. Checking the clock occasionally ensures balance across sections, but obsession with time fractures focus. Let time serve, not suffocate. The well-prepared test taker learns to dance with the clock rather than wrestle against it.
Each question, no matter how complex, deserves a calm gaze. Panic scatters logic. When tension rises, inhale slowly through the nose, exhale through the mouth, and let clarity return. Every deep breath resets the mental compass toward precision and composure.
The Mind After the Storm
When the final section concludes, silence swells in the testing room. Papers rustle, pencils stop, and the invigilator’s voice seems distant. What follows is not mere relief—it is a strange quietness, the mind echoing after hours of concentration. Some students feel triumph, others uncertainty, but all experience transformation. The test becomes a mirror, reflecting months of discipline, endurance, and patience.
The hours of study do not vanish into the air; they remain imprinted upon character. Whether the results exceed expectation or call for improvement, the effort itself is an accomplishment. Success, when achieved, feels like sunrise after long twilight—a blend of gratitude and validation. Yet even a disappointing score holds value. It illuminates the path forward, showing where strength awaits refinement.
Improvement is never failure; it is continuation. Each retake becomes less intimidating because the unknown disappears. Familiarity breeds calm, and calm nurtures excellence. The second attempt often feels like a conversation with an old rival—no longer feared, merely understood.
The key lies in perspective. The THEA, like any test, is not the summit but a milestone. It measures readiness, not worth. Those who grasp this truth walk away unburdened. They recognize that education is not confined to examination halls. The lessons of focus, persistence, and adaptability transcend the boundaries of any single day.
The Broader Journey of Growth
Beyond the test lies a vast landscape of opportunity. College, work, and community life demand the same attributes refined during preparation—discipline, patience, and self-belief. The art of balancing time, managing stress, and sustaining motivation will continue to serve in countless forms. Each page turned in study, each challenge faced, strengthens the foundation upon which future achievements will rise.
In classrooms and careers alike, those who have faced academic trials with courage emerge more resilient. They know the language of effort, the texture of perseverance. They understand that mastery is built upon repetition, reflection, and renewal. The test becomes a rehearsal for life’s wider performances—presentations, interviews, problem-solving, and creative ventures.
The heart of progress lies not in scores but in transformation. A student who once feared complex passages may later craft eloquent essays; one who struggled with timing may become a model of precision in professional tasks. The THEA serves as a bridge between potential and realization. Every challenge overcome in its pursuit leaves behind the imprint of growth.
Within this journey, self-belief becomes the strongest pillar. Confidence is not inherited; it is built through confrontation with uncertainty. Each time a student conquers hesitation, they strengthen the unseen muscles of determination. That same resilience fuels achievements long after the test papers are filed away.
The Landscape of Mind and Emotion
Emotions are the undercurrent of every great effort. Anxiety, excitement, pride, and fear blend in unpredictable proportions. Managing this internal climate becomes an art of self-awareness. The test day magnifies inner voices—one urging caution, another whispering doubt, yet another urging courage. Learning to listen selectively defines success.
The calm mind is not emotionless; it is harmonized. It acknowledges fear but does not obey it. It welcomes confidence without arrogance. Such balance cannot be crammed the night before; it grows from weeks of mindful practice. Meditation, journaling, or simply reflecting on progress help cultivate this equilibrium. The student who understands their emotions transforms them from obstacles into tools.
The body supports the mind’s composure. Proper rest, hydration, and nourishment stabilize mood and energy. Even posture influences perception; a lifted chin and relaxed shoulders communicate readiness not only to observers but to the self. The physical stance becomes a silent declaration of competence.
On test day, emotion and intellect intertwine. The brain may know every formula and rule, yet without composure, knowledge dissolves under stress. Emotional discipline anchors intellectual clarity. The moment one learns to breathe through difficulty, to pause without panic, the test transforms from threat to opportunity.
The Road Beyond the Score
When results arrive, celebration or disappointment may surge, but neither defines the future. Achievement demands acknowledgment, but not complacency. Even victory invites reflection. What habits worked best? What can be refined further? Growth thrives on curiosity.
For those who must retake the exam, the path ahead is familiar and friendlier. The first attempt taught strategy; the next will perfect execution. Every repetition builds mastery, just as musicians refine melody through practice. The goal is progress, not perfection.
Beyond the exam, new horizons unfold. The habits forged—consistent study, balanced living, mindful focus—become lifelong allies. Whether stepping into a college classroom, a workplace, or any pursuit of purpose, these qualities sustain advancement. The student who has weathered the pressures of the THEA walks into the next chapter equipped with sharpened awareness and quiet power.
Communities across the state share this journey of striving and self-betterment. In cities alive with ambition and towns humming with quiet perseverance, students embody the shared dream of advancement. The THEA becomes more than an assessment; it becomes a unifying experience, a testament to endurance and aspiration.
Belief crowns the entire process. The greatest victories occur before a single question is answered—when the student decides that success is possible, that effort has meaning, and that they belong within the walls of achievement. Confidence ignites performance; preparation sustains it.
In the stillness that follows the final bell, pencils rest and hearts steady. The journey has not ended; it has simply changed form. The discipline that conquered distraction, the patience that endured uncertainty, and the courage that faced evaluation all remain, ready to serve in the broader realms of study and life.
The road beyond the THEA stretches wide and luminous. It invites those who have walked through doubt and diligence alike. Each step taken toward readiness now carries the rhythm of mastery, the cadence of confidence, and the grace of perseverance. The path ahead glows with the quiet assurance that every challenge, once embraced, becomes a stepping-stone to greater heights.
Conclusion
Preparing for the THEA is not just about passing a test—it’s about discovering how capable you truly are. Across every section, from reading to writing to mathematics, the process shapes a student into a thinker who can handle challenges with clarity and calm. The exam measures skills, but the preparation builds character.
Each hour of study, every page of notes, and every practice question contribute to something larger than a score. They build patience, confidence, and discipline—the quiet strengths that follow you long after the test ends. The lessons learned while preparing for the THEA are the same lessons that lead to success in college, work, and life itself.
The reading section teaches how to understand ideas deeply and listen to different voices with attention. The writing section reveals the power of clear communication, showing that thoughts become stronger when organized with purpose. The mathematics section trains the mind to see patterns, to reason carefully, and to believe that even the most complex problem can be solved step by step. Together, these lessons form the foundation of true academic readiness.
Texas students who walk this path share more than a goal—they share courage. They decide to meet the challenge head-on, to prepare not just with books but with determination. Every bit of progress proves that success isn’t a matter of talent alone but of persistence and faith in growth.
When the test day arrives and the pencils touch the paper, all the preparation gathers into one powerful moment. It’s the point where effort meets opportunity. Whether the score comes back as expected or calls for another try, the transformation has already happened. You have learned to organize your time, manage your stress, and push beyond limits. Those are victories that no score can measure.
The THEA is a gateway to new beginnings. Passing it opens the doors to higher education, to careers that inspire, and to futures shaped by confidence. But even beyond that, the journey itself reminds every student that learning never truly ends. The skills gained in this preparation become tools for lifelong success.
So as this guide reaches its close, remember that readiness is not a destination—it’s a mindset. With focus, consistency, and belief in your own potential, every test becomes a stepping stone rather than a wall. The road ahead is wide and full of promise, and each Texas student who commits to preparation walks it with strength and purpose.
May every hour of effort turn into opportunity, every moment of doubt into determination, and every dream of success into reality. The ultimate reward of THEA preparation is not just the score—it’s the person you become along the way.
Frequently Asked Questions
How does your testing engine works?
Once download and installed on your PC, you can practise test questions, review your questions & answers using two different options 'practice exam' and 'virtual exam'. Virtual Exam - test yourself with exam questions with a time limit, as if you are taking exams in the Prometric or VUE testing centre. Practice exam - review exam questions one by one, see correct answers and explanations).
How can I get the products after purchase?
All products are available for download immediately from your Member's Area. Once you have made the payment, you will be transferred to Member's Area where you can login and download the products you have purchased to your computer.
How long can I use my product? Will it be valid forever?
Pass4sure products have a validity of 90 days from the date of purchase. This means that any updates to the products, including but not limited to new questions, or updates and changes by our editing team, will be automatically downloaded on to computer to make sure that you get latest exam prep materials during those 90 days.
Can I renew my product if when it's expired?
Yes, when the 90 days of your product validity are over, you have the option of renewing your expired products with a 30% discount. This can be done in your Member's Area.
Please note that you will not be able to use the product after it has expired if you don't renew it.
How often are the questions updated?
We always try to provide the latest pool of questions, Updates in the questions depend on the changes in actual pool of questions by different vendors. As soon as we know about the change in the exam question pool we try our best to update the products as fast as possible.
How many computers I can download Pass4sure software on?
You can download the Pass4sure products on the maximum number of 2 (two) computers or devices. If you need to use the software on more than two machines, you can purchase this option separately. Please email sales@pass4sure.com if you need to use more than 5 (five) computers.
What are the system requirements?
Minimum System Requirements:
- Windows XP or newer operating system
- Java Version 8 or newer
- 1+ GHz processor
- 1 GB Ram
- 50 MB available hard disk typically (products may vary)
What operating systems are supported by your Testing Engine software?
Our testing engine is supported by Windows. Andriod and IOS software is currently under development.